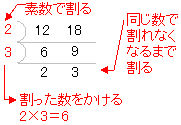
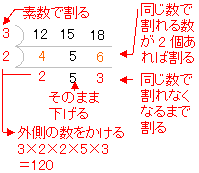
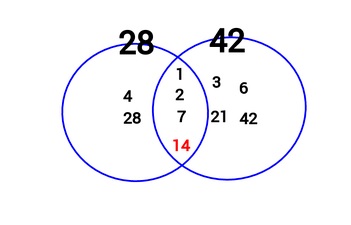
2 50 のような大きな整数の桁数を求めるためには,その常用対数を計算すればよい. (ただし, log 10 2= は分かっているものとする.) log 10 2 50 =50·log 10 2=50 × =1505 ← 公式 (V) log 10 2 50 の整数部分が15だから, 2 50 は16桁の整数 (答) ※対数私が一番印象に残っているのは、2桁の整数に関する性質を帰納的に発見させる授業の展開の仕方に関する内容です。 2桁の整数Aがあって、この数の十の位と数と一の位の数を入れ替えたもう一つの2桁の整数Bとの間には次の性質が成り立ちます。 ① A+Bは ある整数AとBの最大公約数がa,最小公倍数をbとすると となります。 これは、すだれ算を見るとわかります。 最大公約数は2×7 最小公倍数は2×7×2×3 28=2×7×2 42=2×7×3 掛ける順番は違えど、すだれ算の縦列を2回、横列を1回掛けることには変わりありません。
2桁の整数の中で 約数が3個ある数を全て教えてくださいid非 Yahoo 知恵袋
2桁の整数aの約数は
2桁の整数aの約数は-という式が得られた時点で,「2と3が6の約数である」と結論して構わないわけで す。言い替えると,(今の場合2のような)約数が一つ見つかれば,その相棒(今の 場合は3)も約数になっているわけです。 さて6の約数を求めることを続けましょう。B = 0)n に対してa = bk となる整数k が存在す るとき,b はa の約数である,a はb の倍数であるという。 また,a はb で 割り切れるという。 a = bk のとき,a = (b)(k) なので,b がa の約数ならば b もa の 約数である。




高校数学a 約数の個数と総和 約数の対称性と総積 平方数であることの証明 受験の月
ここでは数学Aの「整数の性質」についてまとめています。 「不定方程式」が特に重要であり、「ユークリッドの互除法」や「互いに素」という概念がその解決に役立つでしょう。 目次 1 1節 約数と倍数 11 約数と倍数・倍数の判定方法 12 素因数分解 13算数 割り算ドリルのページへようこそ 上記のボタンから算数割り算ドリル (PDFプリント)がダウンロードできます。 個人利用は無料です (家庭以外での配布は有料です)。 プリント内の数字はランダムです。 大量にありますので、お好きなだけ 下1桁の数(0)が偶数(0は2の倍数に含めるものとする)なので、2の倍数です。 各位の和 である 9が3の倍数なので、3の倍数です。 下2桁 が4の倍数なので、4の倍数です。 下1桁の数 が0なので、5の倍数です。 ここまでで、2の倍数であり3の倍数であることがわかっているので、6の倍
いずれもすでに学習している事柄ですが、これまでよりも応用的な内容となります。 約数と倍数 2つの整数a,bについて、 aがbで割り切れる とき、 bはaの 約数 、 aはbの 倍数 と言います。 たとえば、2つの整数が12,4であれば、12が4で割り切れます。ここで、整数 k を1 桁作るのに使うマッチ棒の本数をnum(k) とすると、Ai を最上位の桁に使えることを調べるには、 dp(N num(Ai)) = dp(N) 1 であるかを調べればよいです。最上位の桁が決まれば、同様に、上から2 番 目、3 番目と上位の桁から順に決めていきます。2 約数の利用 次の式を満たす整数x,y の組(x,y)をすべて求めよ。 (1) xy=4 (2) xy-5x-y=0 整数a と0 でない整数b に対して, a=bk となる整数k があるとき,b はa の 約数 であるという。また,a はb で 割り切れる という。
3桁の自然数2 整数 小学生~中2生対応可能 特に小学生の皆さんに、整数の性質を確認してもらうための問題です。 取り組みやすい大きさである「3桁の 自然数 」を通して調べてみましょう。 問題 「百の位がa、十の位が9、一の位がb」 の3桁の 自然それぞれ10桁の整数 a, b をつくります。 このとき、a b = です。 ただし、例えば4桁の整数5678の上2桁、下2桁を取り出して、 それぞれ2桁の整数c,dをつくると、c=56、d=78、c+d=134です。 7が10個あります次のような整数はいくつできるか? (1)4の倍数 (2)3の倍数 考え方をお願いします。 〔回答〕 ・4の倍数:「下2桁が4の倍数のもの」 ・3の倍数:「各位の数字の和が3の倍数」 と言い換えることができます。 (知らなかった場合は、教科書に載っている



Ie4 Hmk3bevatm
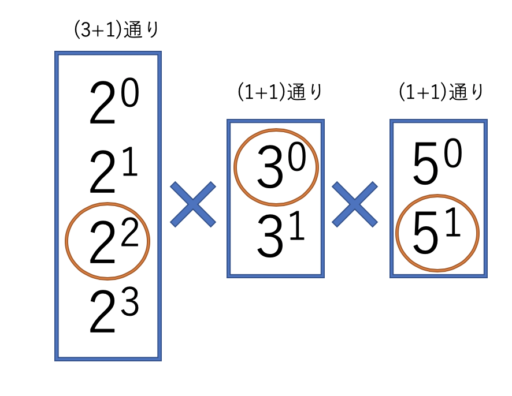



Nの約数の個数を求めるアルゴリズム アルゴリズムロジック
2^ {99}3^ {199} の約数の個数は? 素因数分解されているので,約数の個数は「それぞれの指数に1を足して」「全部かけあわせる」と ( 99 1) ( 199 1) = 000 (991) (1991)=000 (99 1)(199 1) = 000 と分かります。 とてつもなく大きい数なので,約数を全部定理122 二つの整数a, b について(a,b) = d ならばaubv = d を満たす整数の 組(u,v) が存在する。とくに(a,b) = 1 のとき、すなわちa とb が互いに素であるとき、au bv = 1 を満たす組u, v が存在する。 また,逆にau bv = 1 を満たす u, v が存在するならば(a,b) = 1 ,すなわちa, b は互いに素である.整数 約数と倍数 2桁の整数、首位、末位、積 数学のブログ 学び カテゴリーの変更を依頼 記事元 mathmkamimuracom 適切な情報に変更



48s96ub7b0z5f Net Seisuu Yakusuu




数的推理 倍数 約数問題の解答解説してみた 過去問 いい仕事 みつけた
Nは n以下の最大の整数を表す。 † 仮にnが2進法で2'桁とすると、 p nは2進法で'桁である。k 桁の2進数は2k−1 個ある。この場合、和は ∑' k=1 2k−1 £ k(2' ¡)に比例した計算の量となる。これ は' ∑' k=1 2 k−1£ k 以上2' ∑' k=1この中から2 枚選んで隣同士に並 べ、2 桁の整数を作る時、次の各問いに答えなさい。 (1) 作ることができる2 桁の整数は全部で何通りありますか。 2 1 1 12、13、21、23、31、32 の倍数・約数 2つの整数a,bがあって, a=b×q (qは整数) のとき,aはbの倍数,bはaの約数として定義されます。 小学校では,一度に両方の概念を与えると混同しやすいので,別々に扱います。 それで,倍数については,下の例のように,具体的な数をあげて



K Axia2ba1tlgm



Www Ikushin Co Jp Topics Summer Textbook21 Data Kakirensei Shougakuhatten Sansuu Sample02 Pdf
(1)48の約数は全部で 個あります。 (2)50以上の素数で2番目に小さい数は です。 (3)255、459、1122の最大公約数は です。 (4)36、60、84の最小公倍数は です。 (5)2けたの整数で、6の倍数で144の約数でもあるのは 個あります。問1_t3 2,000 の約数の個数として,正しいのはどれか。(東京都13) 1 16 個 2 17 個 3 18 個 4 19 個 5 個 問2_t3 6桁の数1ab8cd について,a,b は0 から9 までの整数のどれかであり,c=9 -a,d=9-bであることが分かっている。整数論の美しい話題です。偶数の完全数の特徴付け,1000桁以下の完全数の一覧など。 完全数とは「約数の総和が自分の2倍になる」ような正の整数 s (a) s(a) s (a) が a a a の異なる約数2



3




Atcoder 版 マスター オブ 整数 素因数分解編 Qiita
小数の割り算 筆算小数第一位までの数÷1桁整数 筆算小数第一位までの数÷1桁整数 (商が1より小さい) 筆算小数第一位までの数÷2桁整数 筆算小数第二位までの数÷整数 筆算2桁の整数で割る(余りを出す)整数の性質(1) ~倍数の判定法,素因数分解~ (1) 2 つの整数a;次のような整数は何個できるか. ⑴ 3桁の整数 ⑵ 3桁で 600以上の整数 ⑶ 4桁の整数の う ち 3の倍 数 18 例題 1 整数をつくる順列 7個の数字0,1,2,3,4,5,6が ある .この中から異なる数字を用いて整数を つくるとき,次のような整数は何個できるか. ⑴ 3




数学1 a 17センター試験 第4問を解いてみよう 日々是鍛錬 ひびこれたんれん



S49rbot8htm4tm
0は整数なのか? ではなく、 0は一桁の整数なのか? ということを聞きたかったんです。 問題集では0を除いていたので気になり質問しました。 また調べてみたのですが、有効桁数と有効数字が関わっているみたいです?約数 約数ある整数を割り切れることができる整数。 18の約数1、2、3、6、9、18 素数約数が1とその数しかない整数 2、3、5、7、11、13、17、までの数の足し算・引き算 2桁の数+1桁の数(繰上なし) この問題の練習をさせたいと思いませんか? 『ポッ! プりんと』は、 何枚でも印刷できます! こちらへ Go!



2桁の整数の中で 約数が3個ある数を全て教えてくださいid非 Yahoo 知恵袋




十の位の数字と一の位の数字の和が9である2けたの整数は9の倍数である このことがらが Clear
このようにして作った整数から無作為に1つの整数を選ぶとき、次の問に答えよ。 (1)2桁の整数が偶数となる確率を求めよ。 (2) 2桁の整数が4の倍数となる確率を求めよ。 (3)2桁の整数が偶数だが4の倍数ではない確率を求めよ。



1




倍数の個数の求め方 数学 苦手解決q A 進研ゼミ高校講座




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ




数aの場合の数についての質問です 数字の0 9を用いてn N 2 桁の整数をつくる Clear




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算




高校数学a 約数の個数と総和 約数の対称性と総積 平方数であることの証明 受験の月




因数分解で大活躍 倍数 約数 の見つけ方



三ケタの整数で約数の個数が5個のものを小学生でも簡単に理解できる方法で解説す Yahoo 知恵袋



ダース についての考察 雑学のソムリエ



約数 倍数の質問です 2ケタの整数aの約数は1およびaとそのほかに3個で合計5 Yahoo 知恵袋



これで大丈夫 素因数分解のやり方と応用




大きな数の最大公約数の求め方 Youtube



約数と倍数 中学受験ー算数解き方ポータル




高校数学a 余りが一致する条件 2乗しても下2桁が変わらない自然数 受験の月



17は素敵な数 算数で考える17 中学受験プロ講師ブログ




中学受験 公 倍数 公 約数の基礎から応用問題まで全部まとめ そうちゃ式 受験算数 新1号館 数論 特殊算




約数の個数の求め方 素因数分解すれば一発で求まる 高校生向け受験応援メディア 受験のミカタ
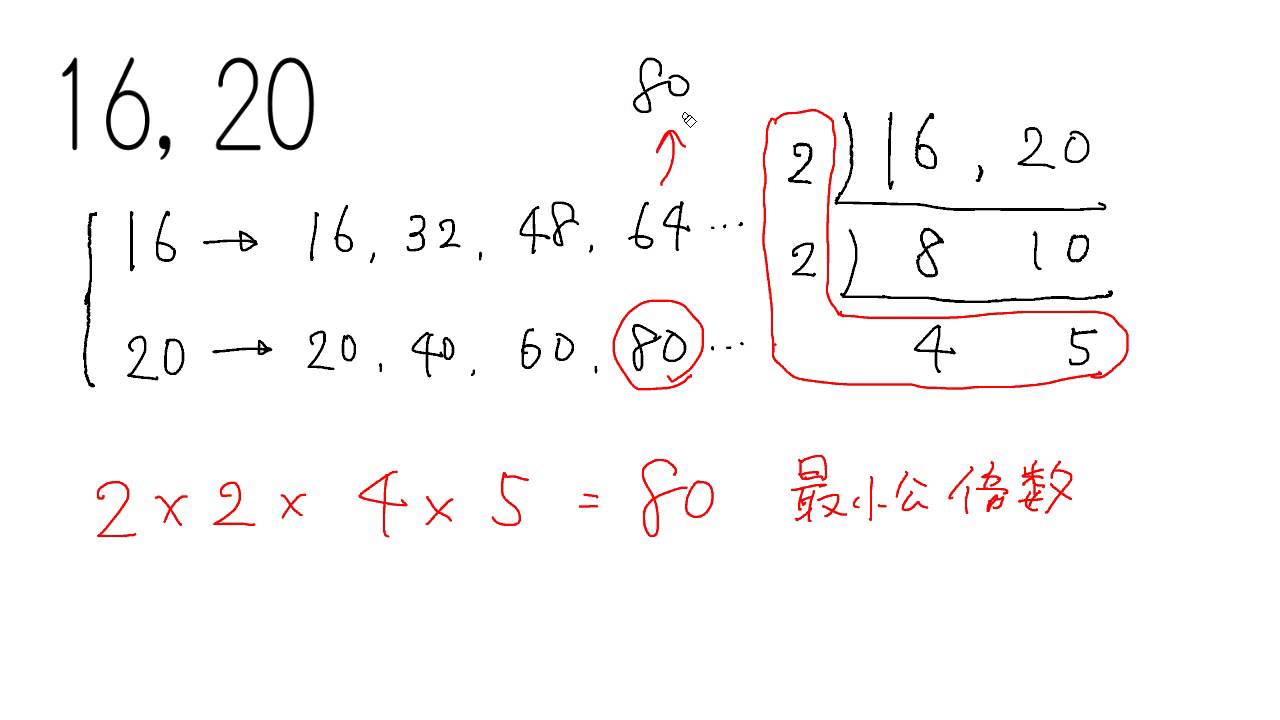



大きな数の最小公倍数の求め方 Youtube




約数と公約数 約数の個数が奇数 平方数 ワンセンテンス算数 Note



解説お願いします 2桁の整数aは1及びaとその他に3個で 合計5 Yahoo 知恵袋
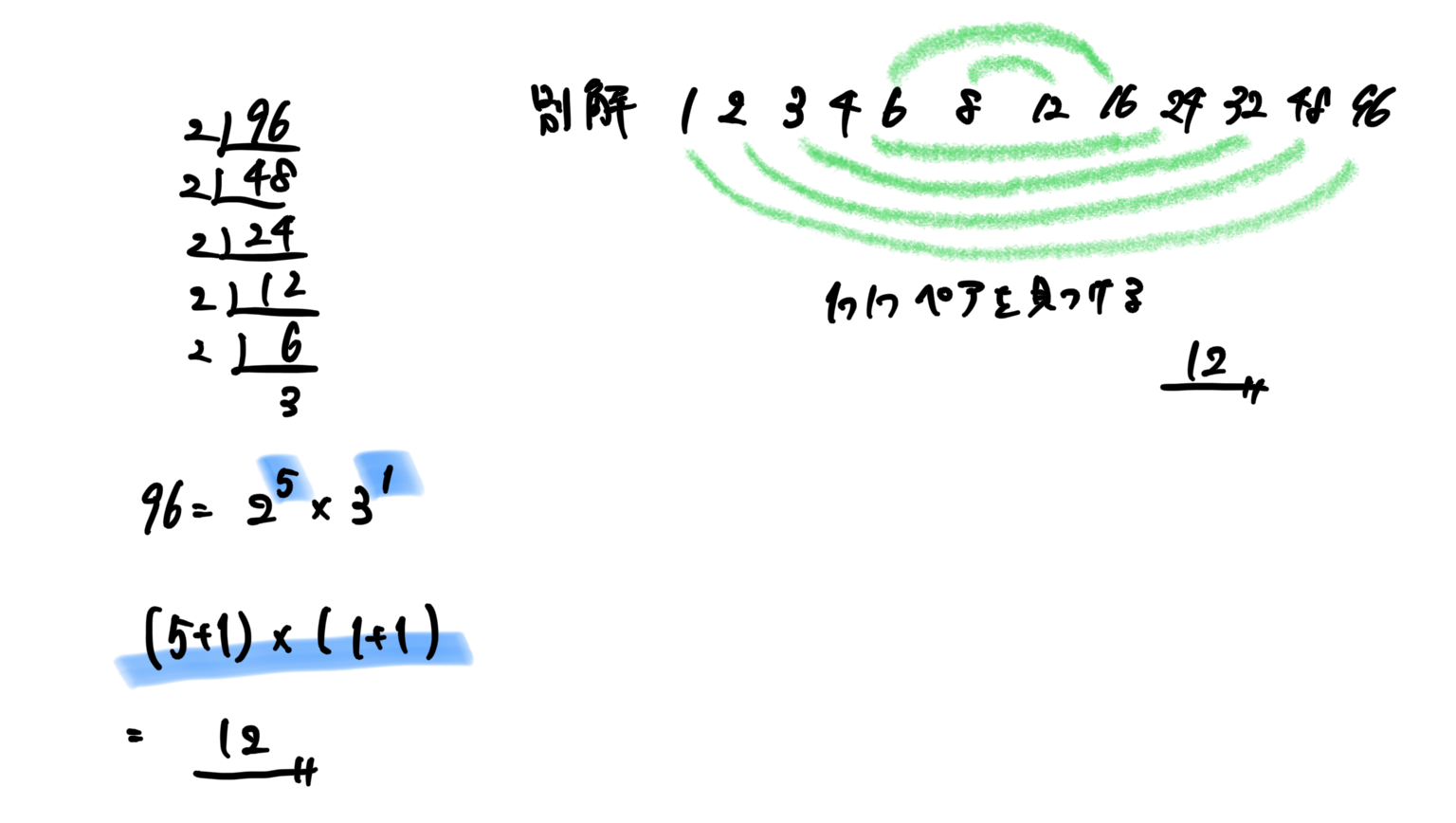



中学受験 約数 倍数 等差数列 周期 受験 ガチ勢 チート Web問題集サイト



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典



Www Metro Ed Jp Hikarigaoka H News 660c7e766afafd8a58ee65fc Pdf




3桁の自然数の中で 次の個数を求めよ という問題なのですが 以下の 数学 教えて Goo



ある2桁の正の整数aには 約数が1とaとその他3個の計5個ある この Yahoo 知恵袋
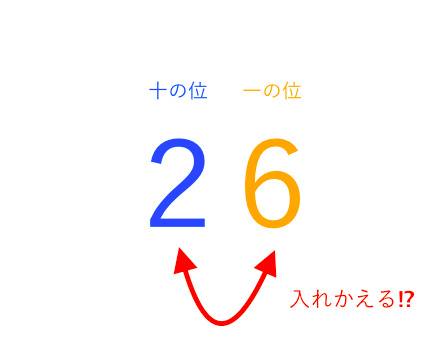



十の位 一の位を入れかえてできる数 苦手な数学を簡単に



Hqippcghatp1em




中学受験 約数の個数の求め方は 素因数分解を活用すれば簡単です そうちゃ式 受験算数 新1号館 数論 特殊算




高校数学a 数字の順列 4桁の奇数 偶数 倍数の個数 受験の月




中学受験 約数 約数の個数 素数 最大公約数と連除法 はしご



問題文は 24の倍数で正の約数が15個であるような自然数を求めよ という Yahoo 知恵袋



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




素因数パズル 1桁 2桁 2桁 1 2 桁 範囲 サイパー思考力算数練習帳シリーズ M Access 本 通販 Amazon




最大公約数の求め方 ユークリッドの互除法 東久留米 学習塾 塾長ブログ




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ




まる付けのために解答が欲しいです 簡単だと思うので誰か解いてみてください Clear




整数 約数の個数 素因数分解 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




暗算の無料プリント 2ケタと3ケタの整数の引き算 全450問 算数パラダイス




超簡単 上から2桁の概数 がいすう で表す 小学校算数 5年生 Yattoke 小 中学生の学習サイト




整数公式 大学受験の王道
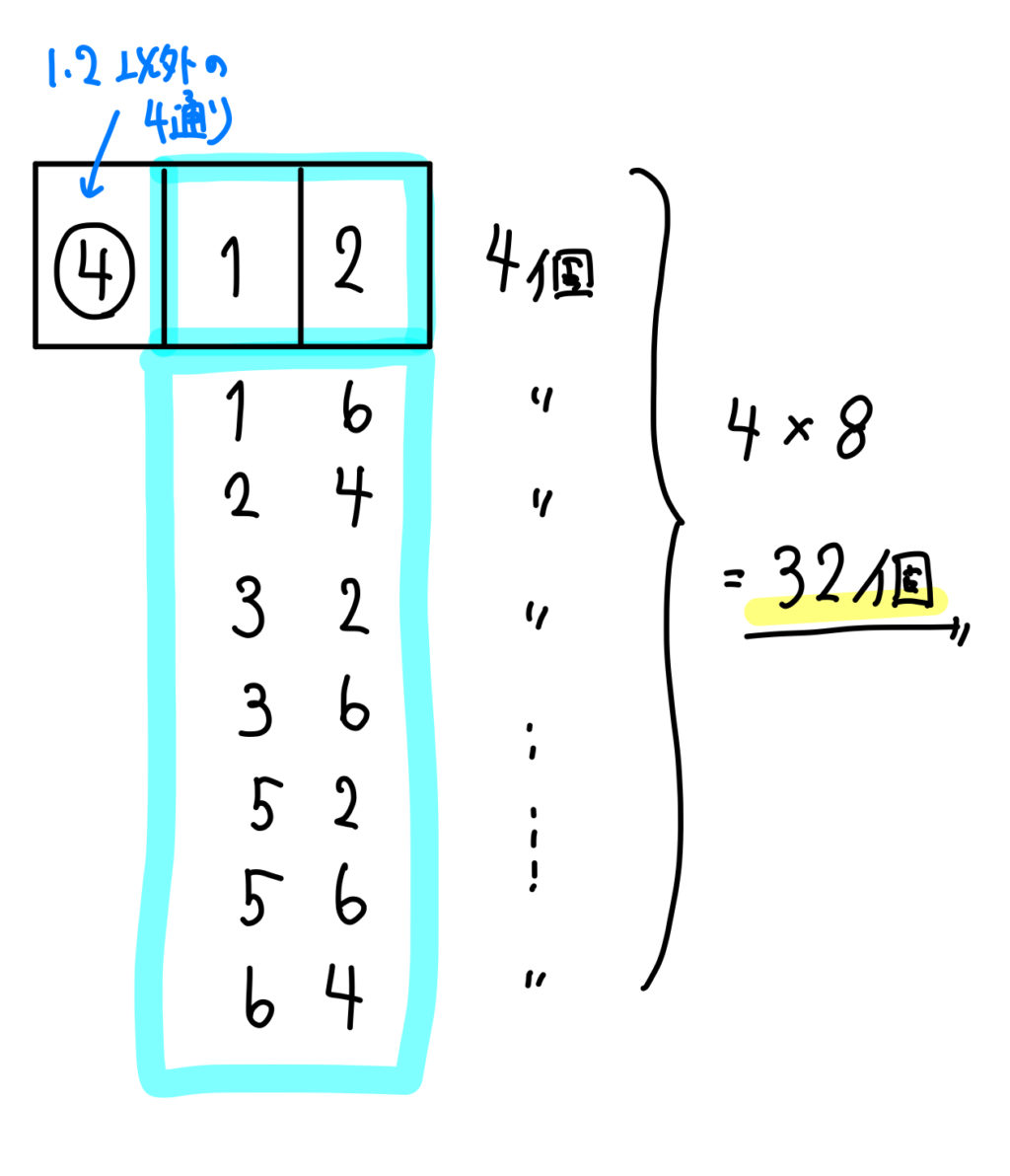



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




倍数と約数の教え方 4 約数の個数 ママのための受験算数の教え方プチ講座 中学受験ナビ



小数 2桁の整数 解答 009 030




最大公約数の求め方 素因数分解を使った解き方のコツとは 高校生向け受験応援メディア 受験のミカタ




図で理解する ユークリッドの互除法 大学入試数学の考え方と解法



最大公約数とは 意味や簡単な求め方 計算問題 受験辞典
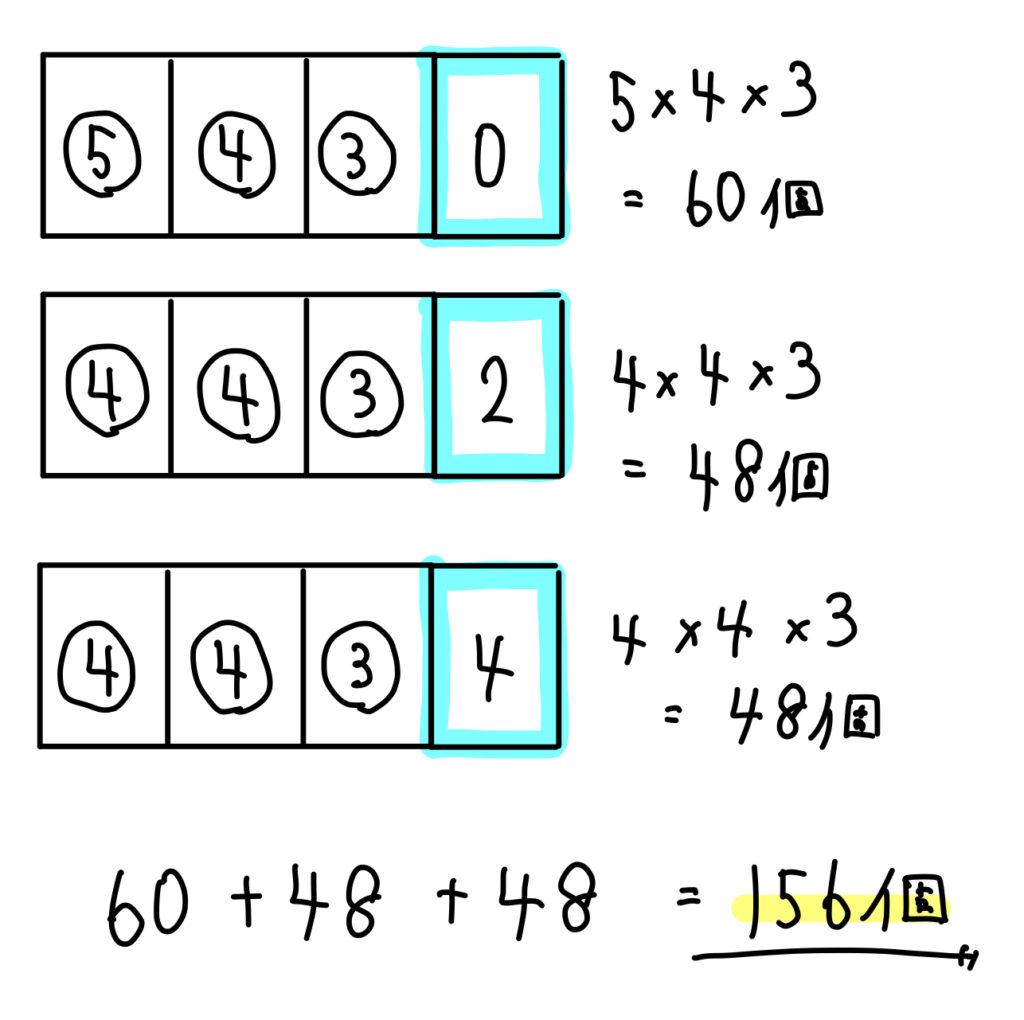



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




公務員試験 地方上級 数的推理 2ケタの整数の約数 魔法陣 倍数の個数 Youtube




順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ



2けたの整数が2つあって その最大公約数が2 2 3 最小公倍 Yahoo 知恵袋



Http Www Min San Com Pd Z5 24 3 Kai




知らないと受験で損をする 倍数の見分け方とその使い道



約数 倍数の質問です 2ケタの整数aの約数は1およびaとそのほかに3個で合計5 Yahoo 知恵袋




6で割っても8 で割っても3 あまる3 けたの整数のうち もっとも小さい数を求めなさい また 48 で割ると33 余り 60 で割ると45 余る最も小さい整数を求めなさい Youtube




高校数学a 3の倍数 9の倍数の見分け方 映像授業のtry It トライイット




倍数と約数について振り返ろう




灘中解説速報 21年第3問 和が5の4桁の数 算数星人のweb問題集 中学受験算数の問題に挑戦




約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典




なぜ互いに素だと10の2乗になるのかよくわからないです Clear




小学5年生の算数 整数の性質 偶数 奇数 約数 倍数 素数 練習問題プリント ちびむすドリル 小学生




小数の掛け算 2桁 3桁 計算ドリル 問題集 数学fun




メルカリ 短期完成 整数の性質ノート 解説編つき 参考書 438 中古や未使用のフリマ



3




裁判所17 約数 倍数 岡野朋一 Note



灘中学算数入試問題にチャレンジ



約数 倍数




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ



Mathtext Info Sansuu Sansuu Suu K 52 Pdf




5年算数 整数の性質 公倍数 公約数 の簡単な求め方 マドリト フリーランスデザイナーのブログ



約数 倍数
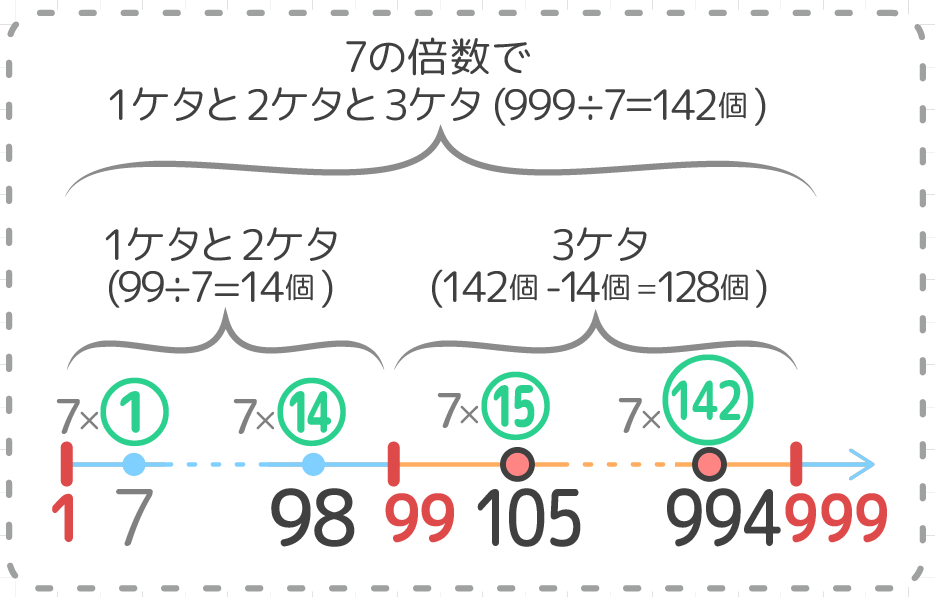



小学生 倍数の個数の求め方 2ケタ 3ケタ等 中学受験頻出 そうちゃ式 受験算数 新1号館 数論 特殊算




約数の求め方 素因数分解 問題 98の約数を求めなさい ただし 2ケ 数学 教えて Goo




の質問です なぜ解答の下線部のようになるのか分かりません Clear




数学です 教えてほしいです Clear




小学4年生 算数 無料問題集 小数 100分の1の位まで 1桁の整数の掛け算の筆算 おかわりドリル




数a 28の倍数で正の約数の個数が15こである自然数nを全て求めよ とい 数学 教えて Goo



2桁の整数のうち 4の倍数で72の約数であるものは何個あるか 私の答えは Yahoo 知恵袋



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典




速算 二桁の整数の積を速く計算する方法 証明付き 大学入試数学の考え方と解法



17年センター試験数学1a大問4 ほのぼの数学頑張ろう



約数とは 約数の個数や総和の求め方 約数表 計算問題 受験辞典



数学の質問です 2桁の自然数で 約数を最も多く持つもの Yahoo 知恵袋




分数の約分のやり方と教え方のコツ 時間短縮に便利なテクニックを紹介 数学fun



たくさんの約数を持つ数 雑学のソムリエ




最高 最小 公倍数 問題




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




1講 約数と倍数 1節 約数と倍数 問題集 3章 整数の性質




学校では教えてくれない約数 公約数の上手い見つけ方 Youtube



最大公約数の求め方 すだれ算 中学受験 塾なし の勉強



Q Tbn And9gcrz4tiiujvjvtvxv2ozmm Mvsq9zohcodw0yyuasqa Asxohv5b Usqp Cau




上から2けたのがい数で表す Youtube



0 件のコメント:
コメントを投稿